Spherical Dome Calculator
Using the Spherical Dome Calculator
The MDI Spherical Dome Calculator helps calculate common design elements of a partial sphere set on an optional stem wall. It helps with quick design ideas as well as provides accurate measurements when finalizing structural elements. Outputs include circumference, surface area, volume, and distances along and around the building’s various details.
A level input measures a slice of the structure. For example, it can calculate the area of a second floor, show headroom around the dome perimeter, or calculate the volume and surface area of a portion of the dome.
All parameters are stored in the page URL which may be bookmarked, saved, and shared. Use “Copy to Clipboard” to copy-and-paste results into your notes or emails. Print page or save as PDF for a professional copy of the drawing and results.
Be aware that just because the calculator can draw a structure, it does NOT mean the structure can be built. This calculator is just a tool. Always consult with qualified professionals before proceeding with a project.
This calculator is subject to our Terms of Service.
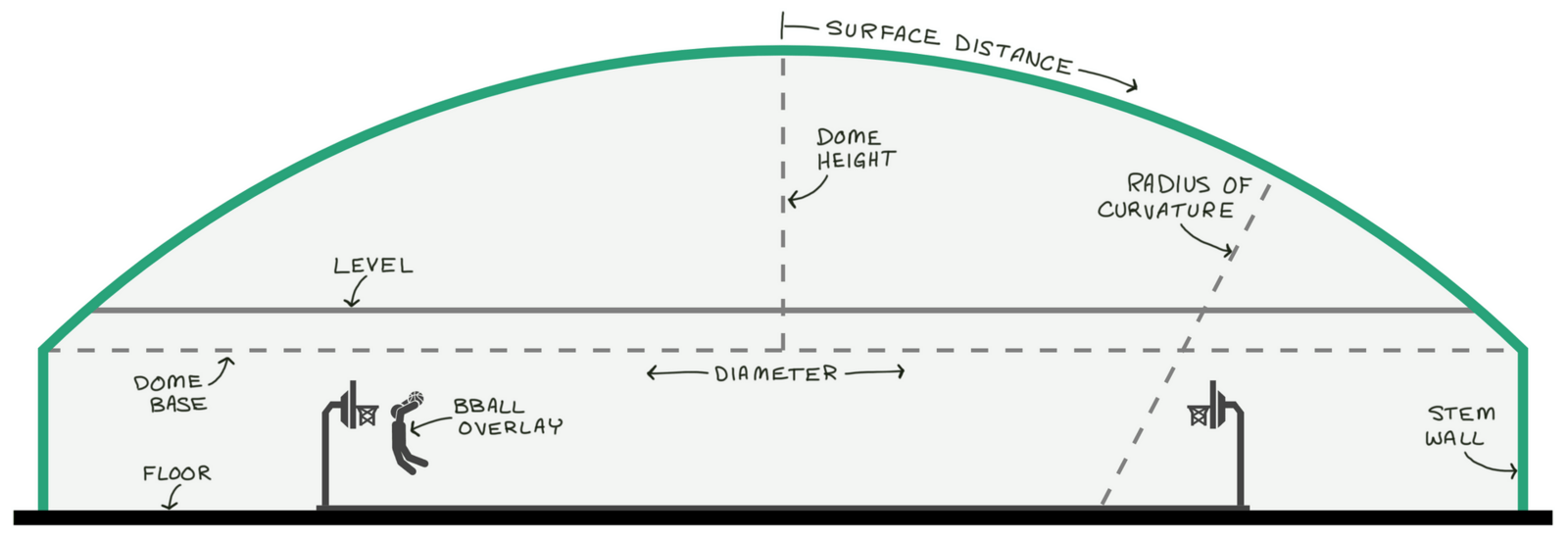
A complete spherical dome calculation including a basketball court overlay and the imaginary ceiling level for the required distance of play over the court. This is based on the Italy High School Multipurpose Center built using a spray-in-place concrete stem wall. The calculated dome is 148-feet diameter, 30-feet tall, on a 16-foot tall stem wall. Click for the live calculator version of this gymnasium!
Inputs
Diameter. The overall diameter of the structure. The calculator applies the diameter to the floor, stem wall, and base of the spherical dome. A single diameter input is useful for quick estimates, but when calculating a specific design that may have a different diameter for the stem wall, you should run two separate calculations.
Height. The height of the spherical dome from its base to the apex.
Stem Wall. The height of the stem wall extends vertically from the circular floor to the base of the dome. The stem wall height is optional by leaving the height set to zero (0).
Level. The optional horizontal level above the floor forms a subsection of the structure. It calculates an imaginary circle at that level plus the upper portion of the structure from that level to the apex.
Overlay. A scaled, graphical overlay to assist in visually representing the building size and purpose.
Units. The selectable unit will label the calculator outputs and properly scale the overlay. Note that all numerical inputs must be given in the same selected unit.
Floor
Diameter. The floor diameter is a circle representing the floor, stem wall, and dome base diameter.
Radius. The floor radius is half the floor diameter and is a useful number for various calculations.
Circumference. The floor circumference is the distance around the circle-shaped floor, stem wall, and dome base.
Area. The floor area is the area of the circle inscribed by the floor diameter.
Dome
Height. The dome height is the distance from the base of the dome to the apex.
Radius of Curvature. All dome structures described by this calculator are a segment or “cap” of a sphere as defined by the dome’s diameter and height. The radius of curvature is the calculated radius of the whole sphere of which the dome is a portion.
Surface Distance. The dome surface distance is the length from the apex, following the dome curve down to the dome base.
Surface Area. The dome surface area is technically the dome’s lateral surface area from the base to the apex.
Volume. The dome volume is the cubic measure of the volume encompassed by the structure’s dome portion.
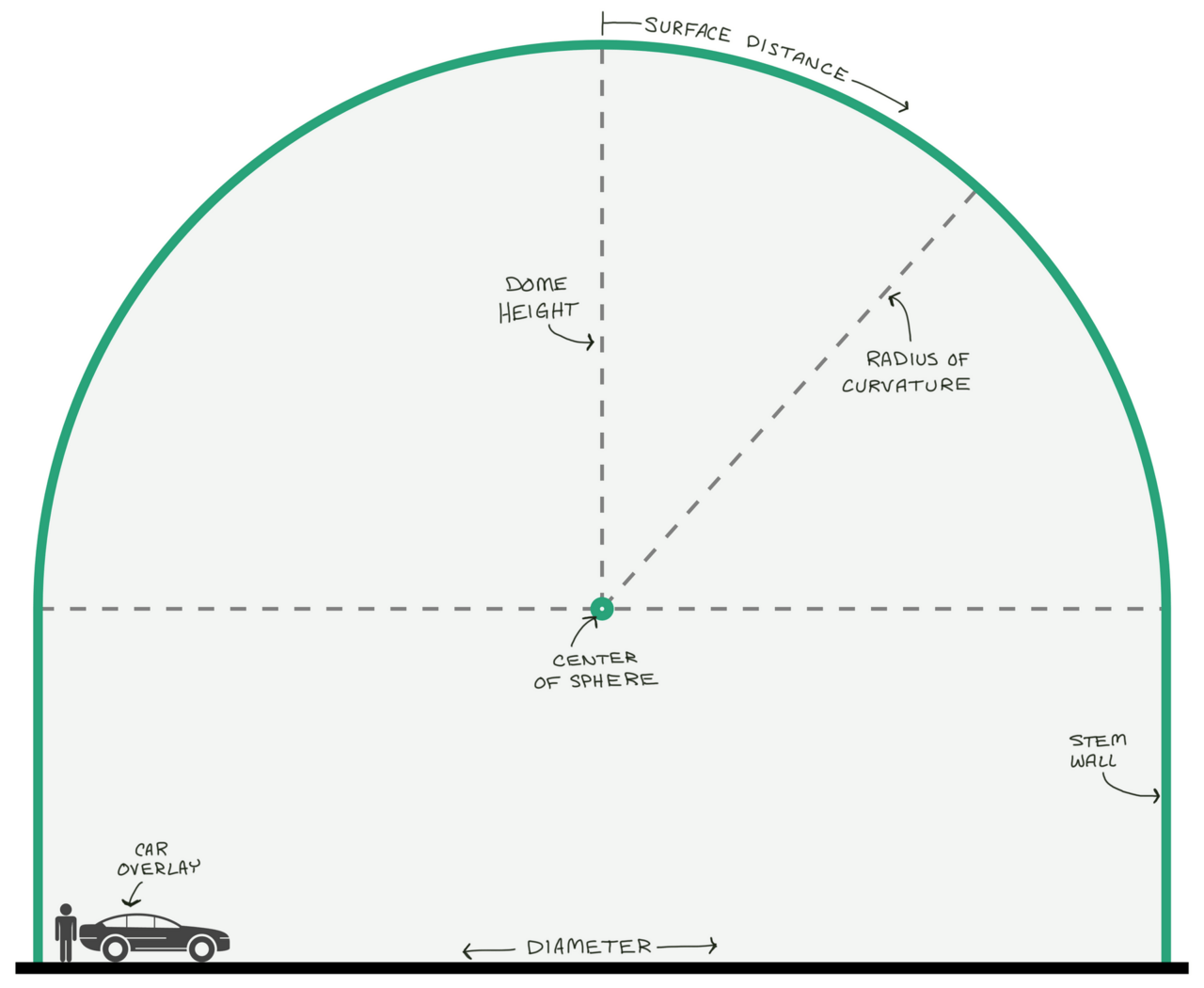
The spherical calculation of the Elkhart Ammonium Nitrate Storage. It is a 115-foot diameter hemisphere with a 36-foot tall stem wall integrated into the inflatable Airform membrane with the car overlay to show scale. Click for the live calculator version of this storage!
Stem Wall
Height. The stem wall height describes a cylinder’s height with the floor diameter and the stem wall height. It connects the floor to the dome base. Leave the stem wall height set to zero (0) to remove the stem wall.
Surface Area. The stem wall surface area is the area of the cylinder formed by the stem wall.
Volume. The stem wall volume is the cubic measure of the volume encompassed by the stem wall cylinder.
Total
Height. The total height is the overall height of the structure, as defined by the sum of the stem wall and dome heights.
Surface Distance. The total surface distance is the dome surface distance from the apex to base plus the height of the stem wall equaling the distance along the surface of the building from the apex to the floor.
Surface Area. The total surface area is the sum of the dome surface area plus the stem wall cylinder surface area.
Volume. The total volume is the cubic measure of the total volume encompassed by the complete structure.
Level @
Height Above Floor. The level height is the distance from the floor to a horizontal “slice” at the level specified above the floor. It effectively creates a subsection of the overall building.
Diameter. The level diameter is the calculated diameter at the specified level above the floor.
Radius. The level radius is the calculated radius—half the level diameter—at the specified level above the floor.
Circumference. The level circumference is the perimeter around the imaginary slice at the level specified above the floor.
Area. The level area is the area of the circle described by the imaginary slice at the level specified above the floor. A common use is to set the level at 10-feet (3 m) to calculate the second floor’s diameter and area.
Portion Above Level
Remaining Height. The imaginary slice through the structure at the specified level essentially creates a second portion of the overall structure. The remaining height is calculated as the height from the specified level to the apex of the dome.
Surface Distance. The level surface distance is the overall surface distance from the dome apex to the imaginary slice at the specified level. It will correctly follow the dome and even down the stem wall.
Surface Area. The level surface area is the remaining structure’s overall surface area above the imaginary slice at the specified level. It’s a surprisingly useful measure when calculating material needs for a dome.
Volume. The level volume is the total cubic volume encompassed by the remaining structure above the specified level.
Overlays
An overlay is a scaled illustration to help convey the size, purpose, and scope of the calculated structure. They are for convenience only. No attempt is made to “fit” them inside the building or to determine their appropriate use for a structure. They are merely a visual aid.
None. The none option deletes the overlay.
Person. The person overlay is the default overlay. It is a person rendered at 6-feet (1.8 m) tall.
Car. The car overlay is a mid-sized sedan with a 6-foot (1.8 m) person standing beside it.
BBall. The bball overlay is the side silhouette of a standard American competition basketball court on a six-inch floor. We recommend setting the level parameter to 20.5 feet to show the standard clearance height required for a competition floor.
Loader. The loader overlay is a small front-end loader—6,000 pounds (2800 kg) operating capacity with bucket—approximately 8 feet (2.5 m) tall next to a 6-foot (1.8 m) tall person.
Heavy. The heavy overlay is a large front-end loader—66,000 pounds (30,000 kg) operating weight—approximately 12.5 feet (3.8 m) tall next to a 6-foot (1.8 m) tall person.
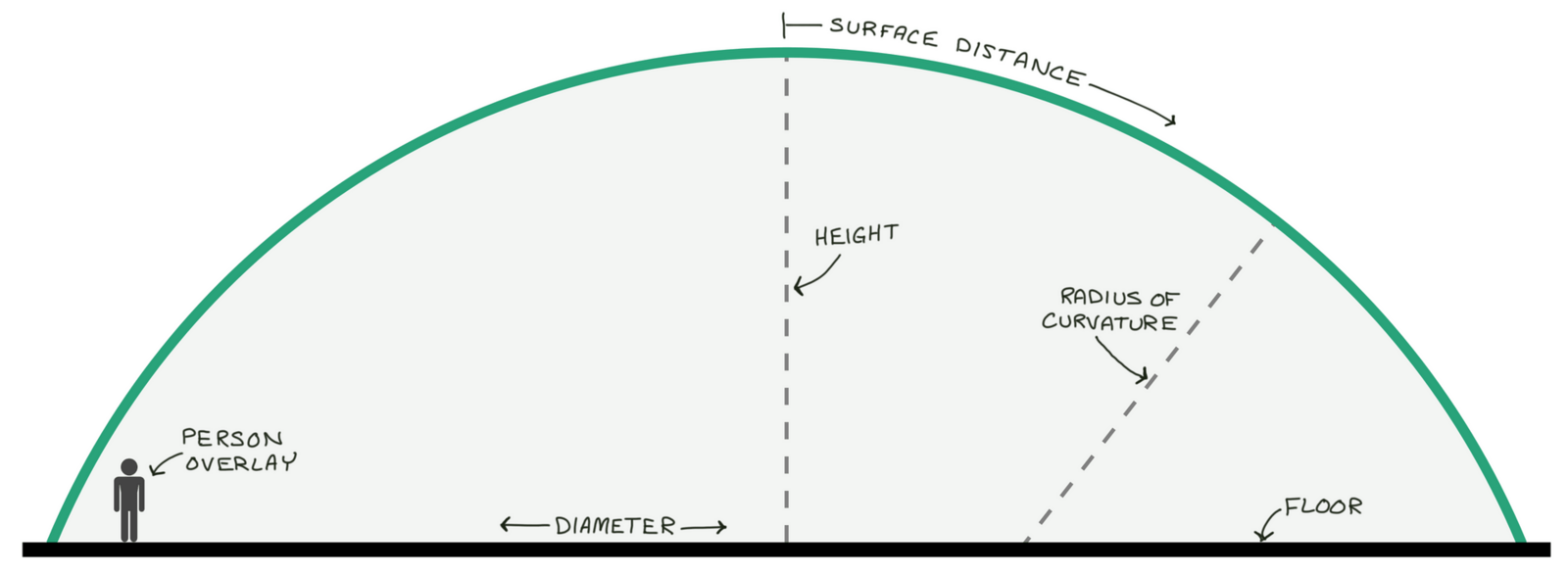
The spherical calculation of the First Monolithic Dome constructed in Shelley, Idaho. It is a 105-foot diameter by 35-foot tall dome. You can see from the person overlay that it was also very ambitious for a first structure. This is the default structure created by the calculator. Click for the live calculator version of this first dome!