Ellipsoid Dome Calculator
Using the Ellipsoid Dome Calculator
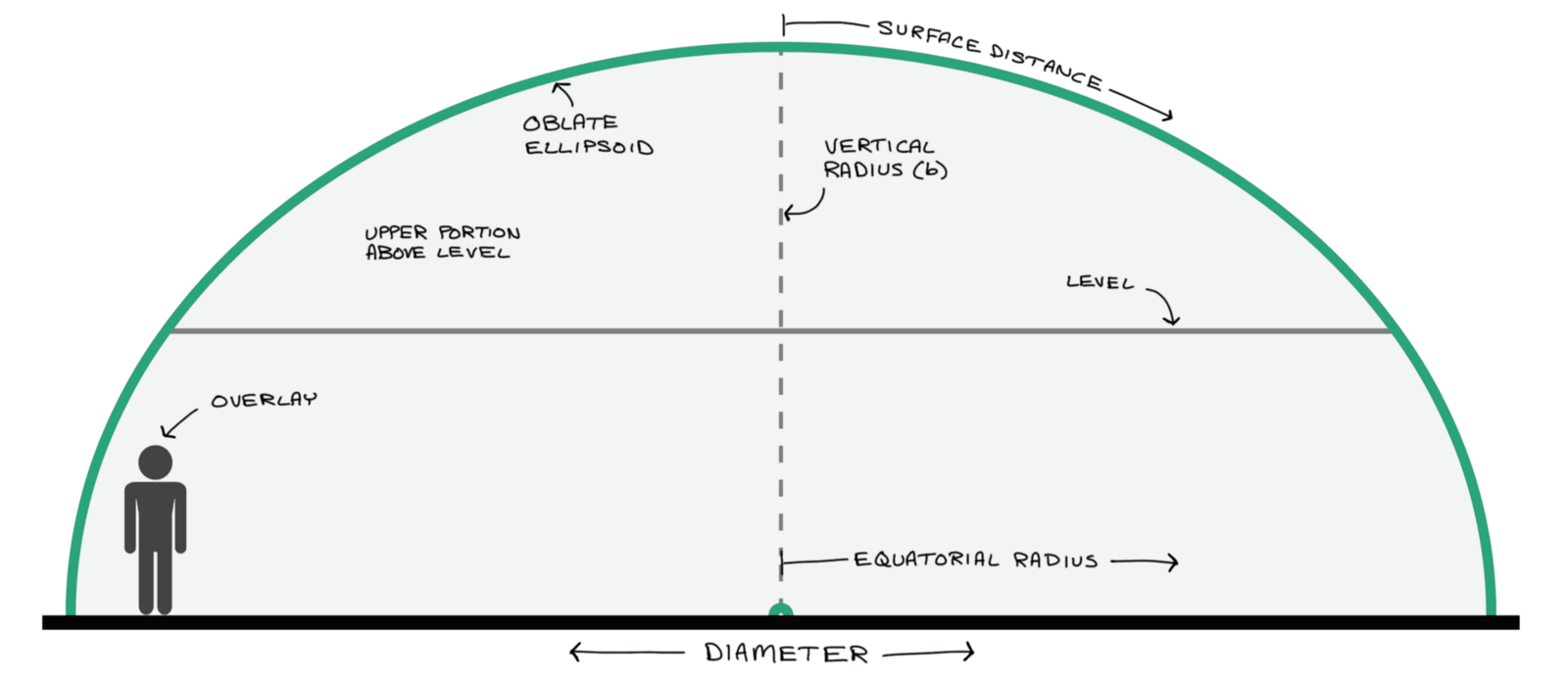
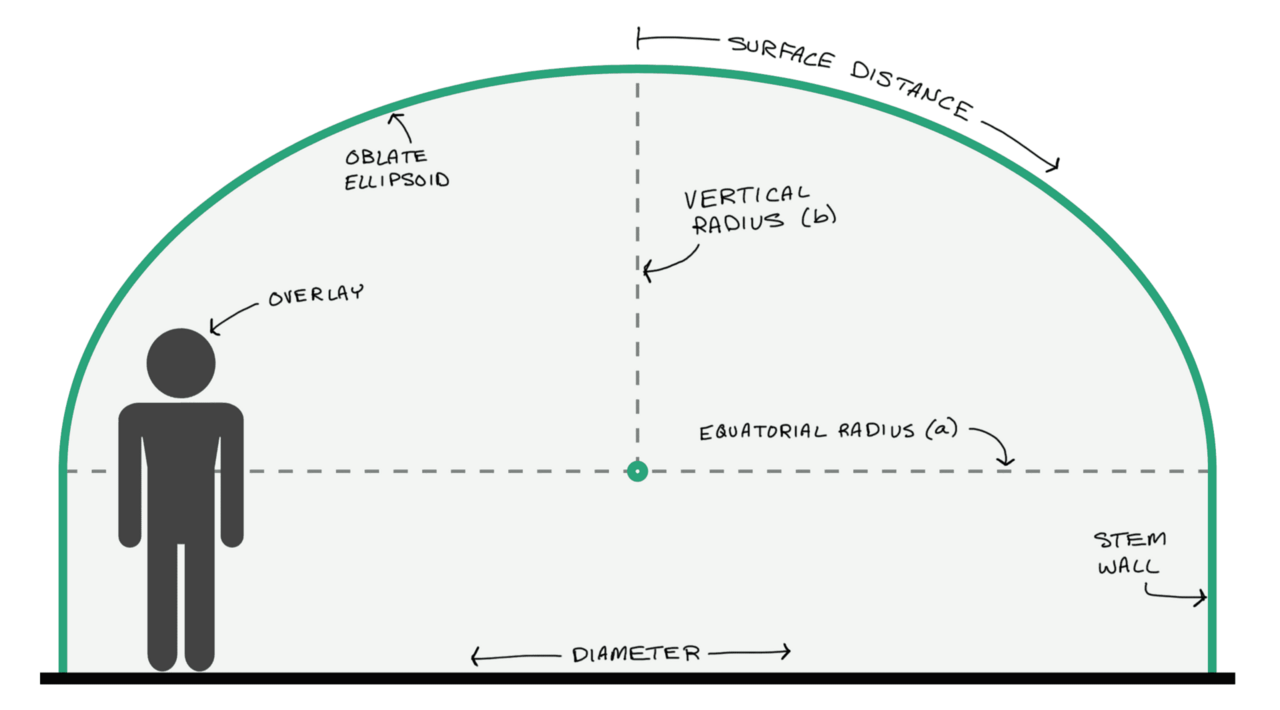
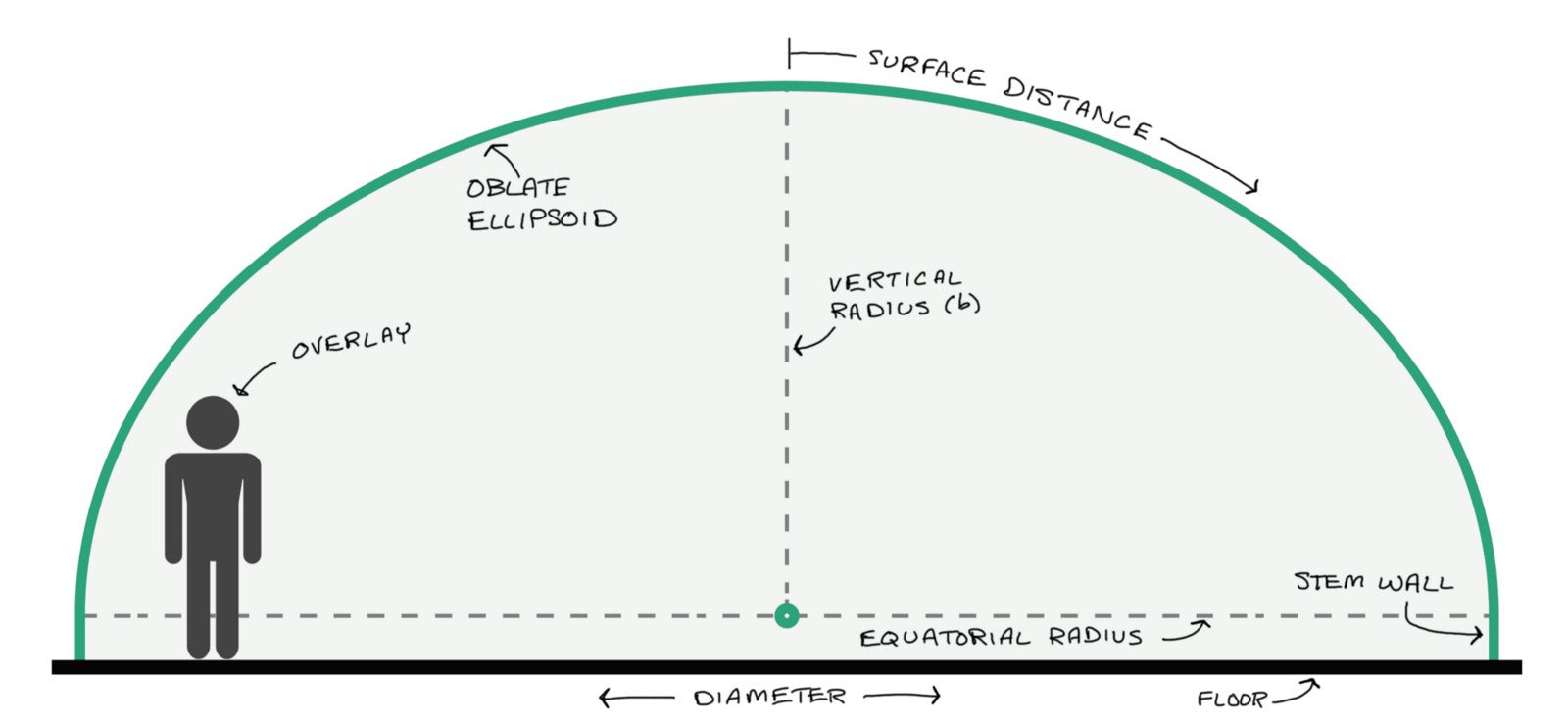
Half ellipsoid domes are commonly used for house-sized structures. The oblate ellipsoid—a dome that looks a little like someone sat on it—has a circular foundation and an elliptical cross-section. The shape lowers the overall height while providing more “headroom” against the dome “wall.” It can reduce the surface area—lowering the price and providing more effective floor space—compared to similar spherical dome designs.
Less common than oblate ellipsoids, prolate ellipsoids are tall shapes often used for specialized rooms in multi-dome construction. Where an oblate ellipsoid has a height less than the radius of the base, the prolate ellipsoid height is taller than the radius of the base. Both are supported by this calculator. Hemisphere calculations are also supported, but we recommend using the Spherical Dome Calculator instead.
All parameters are stored in the page URL which may be bookmarked, saved, and shared. Use “Copy to Clipboard” to copy-and-paste results into your notes or emails. Print page or save as PDF for a professional copy of the drawing and results.
Be aware that just because the calculator can draw a structure, it does NOT mean the structure can be built. This calculator is just a tool. Always consult with qualified professionals before proceeding with a project.
This calculator is subject to our Terms of Service.
A half-ellipsoid dome calculation for a large three-bedroom Monolithic Dome home. The dome is 50-feet in diameter by 20-feet tall with a 10-foot floor level added for a potential loft. The elliptical cross-section of this oblate ellipsoid flattens the top while creating more headroom around the base. Click for the live version of this design.
Inputs
Diameter. The maximum circular base dimension of the dome and optional stem wall. The radius of the base—half the diameter—is the equatorial radius (a) of the ellipsoid. The maximum recommended diameter is 100 feet (30 m).
Height. The height of the ellipsoid portion of the structure. It is the vertical radius (b) of the ellipsoid.
Stem Wall. The height of the optional stem wall cylinder. Set wall height to zero (0) to remove stem wall calculations.
Level. The optional horizontal level above the floor, forming a subsection of the structure. It calculates an imaginary circle at that level plus the upper portion of the structure from that level to the apex. The level is useful for calculating the second floor.
Overlay. A scaled, graphical overlay to assist in visually representing the building size and purpose.
Units. The selectable unit will label the calculator outputs and properly scale the overlay. Note that all numerical inputs must be given in the same selected unit.
Floor
Diameter. The floor diameter is a circle representing the floor, stem wall, and dome base diameter.
Radius. The floor radius is half the floor diameter and is a useful number for various calculations.
Circumference. The floor circumference is the distance around the circle-shaped floor, stem wall, and dome base.
Area. The floor area is the area of the circle inscribed by the floor diameter.
Dome
Height. The dome height is the distance from the base of the dome to the apex.
Ellipticity Ratio. The ratio between the equatorial radius and vertical radius describing the cross-section ellipse. A ratio greater than one is an oblate ellipsoid and less than one is a prolate ellipsoid. The maximum recommended oblate ellipsoid ratio is 1.45—the Airform membrane begins to wrinkle at ratios higher than 1.45.
Curvature. The radius of curvature is a measure of the curve itself at the top. The distance is from the curve to an imaginary origin that would describe a sphere of that same curvature.
Surface Distance. The dome surface distance is the length from the apex, following the dome curve down to the dome base.
Surface Area. The dome surface area is technically the dome’s lateral surface area from the base to the apex.
Volume. The dome volume is the cubic measure of the volume encompassed by the structure’s dome portion.
The Io-20 studio apartment is a common design built at the Monolithic Dome Builders Workshop. It’s an oblate ellipsoid, 20-feet in diameter by 7-feet tall on a 3.5-foot stem wall. Click for live calculator version of this design.
Stem Wall
Height. The stem wall height describes a cylinder’s height with the floor diameter and the stem wall height. It connects the floor to the dome base. Leave the stem wall height set to zero (0) to remove the stem wall.
Surface Area. The stem wall surface area is the area of the cylinder formed by the stem wall.
Volume. The stem wall volume is the cubic measure of the volume encompassed by the stem wall cylinder.
Total
Height. The total height is the overall height of the structure, as defined by the sum of the stem wall and dome heights.
Surface Distance. The total surface distance is the dome surface distance from the apex to base plus the height of the stem wall equaling the distance along the surface of the building from the apex to the floor.
Surface Area. The total surface area is the sum of the dome surface area plus the stem wall cylinder surface area.
Volume. The total volume is the cubic measure of the total volume encompassed by the complete structure.
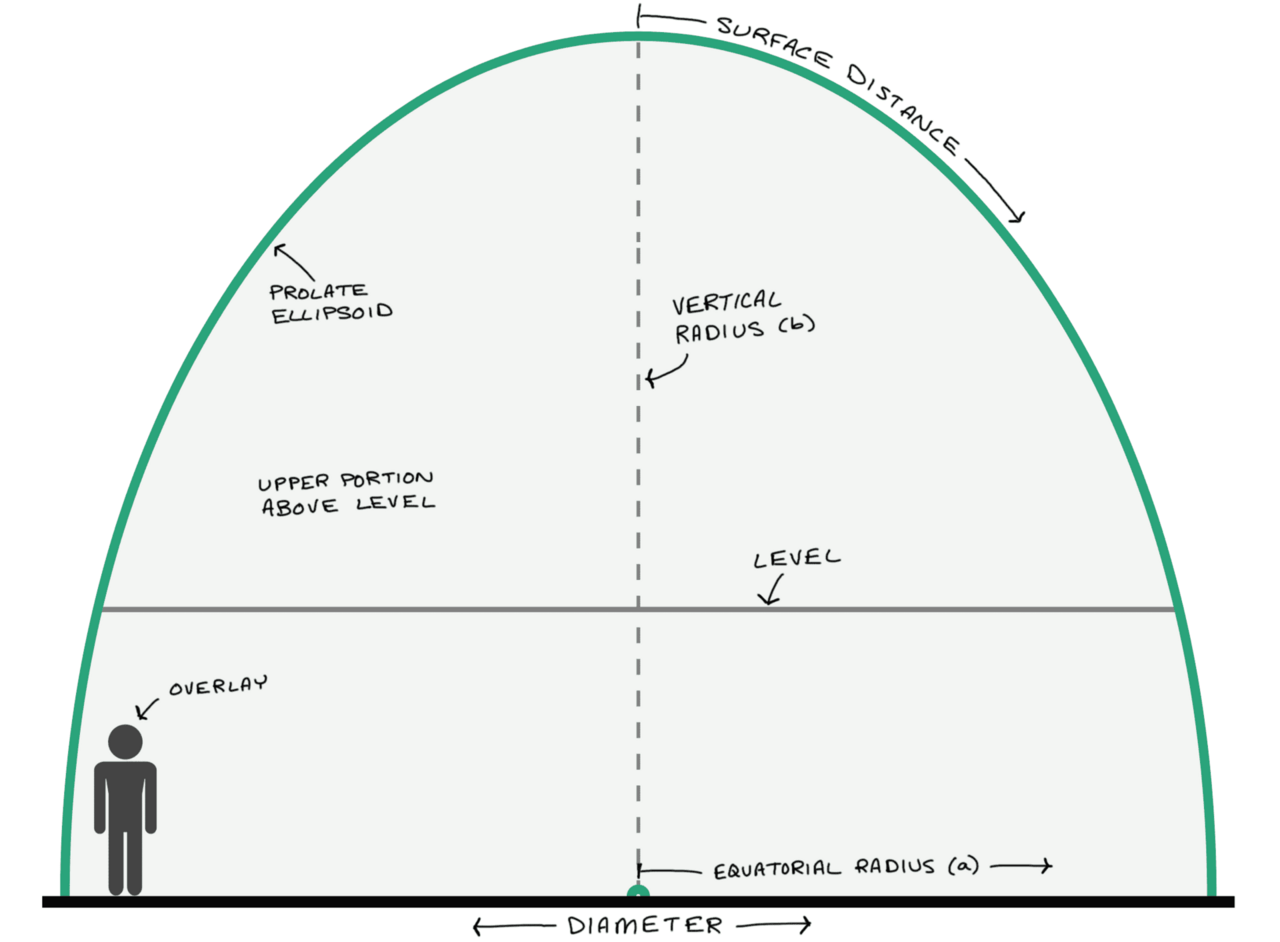
An example of a prolate ellipsoid—40-feet in diameter by 30-feet tall. A second floor level at 10-feet is shown. By running the calculations twice with a 10-foot level and 20-foot level, we find a dome shape with a maximum potential floor area of over 3,000 square feet. Click for live calculator version of this design.
Level @
Height Above Floor. The level height is the distance from the floor to a horizontal “slice” at the level specified above the floor. It effectively creates a subsection of the overall building.
Diameter. The level diameter is the calculated diameter at the specified level above the floor.
Radius. The level radius is the calculated radius—half the level diameter—at the specified level above the floor.
Circumference. The level circumference is the perimeter around the imaginary slice at the level specified above the floor.
Area. The level area is the area of the circle described by the imaginary slice at the level specified above the floor. A common use is to set the level at 10-feet (3 m) to calculate the second floor’s diameter and area.
Portion Above Level
Remaining Height. The imaginary slice through the structure at the specified level essentially creates a second portion of the overall structure. The remaining height is calculated as the height from the specified level to the apex of the dome.
Surface Distance. The level surface distance is the overall surface distance from the dome apex to the imaginary slice at the specified level. It will correctly follow the dome and even down the stem wall.
Surface Area. The level surface area is the remaining structure’s overall surface area above the imaginary slice at the specified level. It’s a surprisingly useful measure when calculating material needs for a dome.
Volume. The level volume is the total cubic volume encompassed by the remaining structure above the specified level.
Overlays
An overlay is a scaled illustration to help convey the size, purpose, and scope of the calculated structure. They are for convenience only. No attempt is made to “fit” them inside the building or to determine their appropriate use for a structure. They are merely a visual aid.
None. The none option deletes the overlay.
Person. The person overlay is the default overlay. It is a person rendered at 6-feet (1.8 m) tall.
Car. The car overlay is a mid-sized sedan with a 6-foot (1.8 m) person standing beside it.
BBall. The bball overlay is the side silhouette of a standard American competition basketball court on a six-inch floor. We recommend setting the level parameter to 20.5 feet to show the standard clearance height required for a competition floor.
Loader. The loader overlay is a small front-end loader—6,000 pounds (2800 kg) operating capacity with bucket—approximately 8 feet (2.5 m) tall next to a 6-foot (1.8 m) tall person.
Heavy. The heavy overlay is a large front-end loader—66,000 pounds (30,000 kg) operating weight—approximately 12.5 feet (3.8 m) tall next to a 6-foot (1.8 m) tall person.
The Oberon dome home is 32-feet in diameter by 12-feet tall on a 1-foot stem wall. The oblate ellipsoid shape lowers the overall height while providing more usable floor space around the perimeter. Click for live calculator version of this design.