Ellipse Calculator
Using the ellipse calculator
The Monolithic Dome Institute Ellipse Calculator is a simple calculator for a deceptively complex shape. It will draw and calculate the area, circumference, and foci for any size ellipse. It’s easy to use and easy to share results.
Input the major-radius, minor-radius, and the preferred units and press “Go.” It will draw the ellipse and output the calculations. The page URL will save the values and can be bookmarked or shared with others. Use the “Copy to Clipboard” to quickly copy and paste results in emails, messages, or research notes.
This calculator is subject to our Terms of Service.
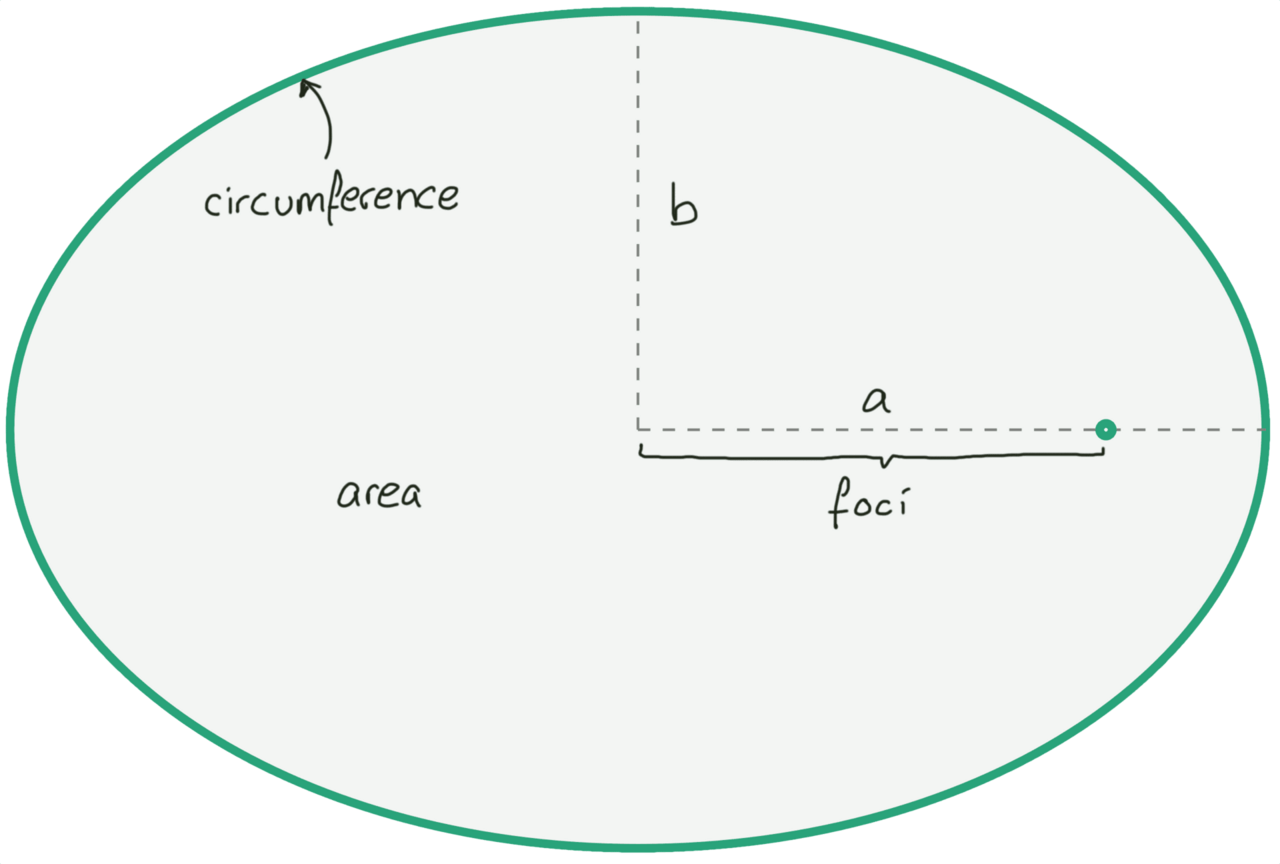
Diagram of the default ellipse calculator results with the major radius (a) and minor radius (b) plus one focal point (foci).
Major radius. The major radius, the semi-major axis, or “a” of the ellipse is the distance from the coordinate center to the furthest point on the ellipse. It is half the major diameter, major-axis, or “A” of the ellipse.
Minor radius. The minor radius, the semi-minor axis, or “b” of the ellipse is the distance from the coordinate center to the closest possible point on the ellipse. It is half the minor diameter, minor-axis, or “B” of the ellipse. The minor-axis is always perpendicular to the major axis.
Circumference. The circumference is the perimeter around the ellipse. There are many formulas developed to approximate the circumference with varying levels of accuracy. This calculator uses “Infinite Series 2” found on the Math is Fun website. It uses 20 binomial coefficient terms for the approximation and is quite accurate for large elliptical footprints.
Curvature. The radius of curvature is a measure of the curve itself at the minor (b) vertex. The distance is from the curve to an imaginary origin that would describe a circle of that same curvature.
Area. The area of the ellipse using the formula A = πab.
Foci. The distance from the coordinate center on the major-axis—both directions—to the elliptical focal points. Use the foci distance plus the pin and string method to draw an ellipse on paper or on a job site.
Units. The unit selection is for output formatting, only.
This calculator is subject to our Terms of Service.
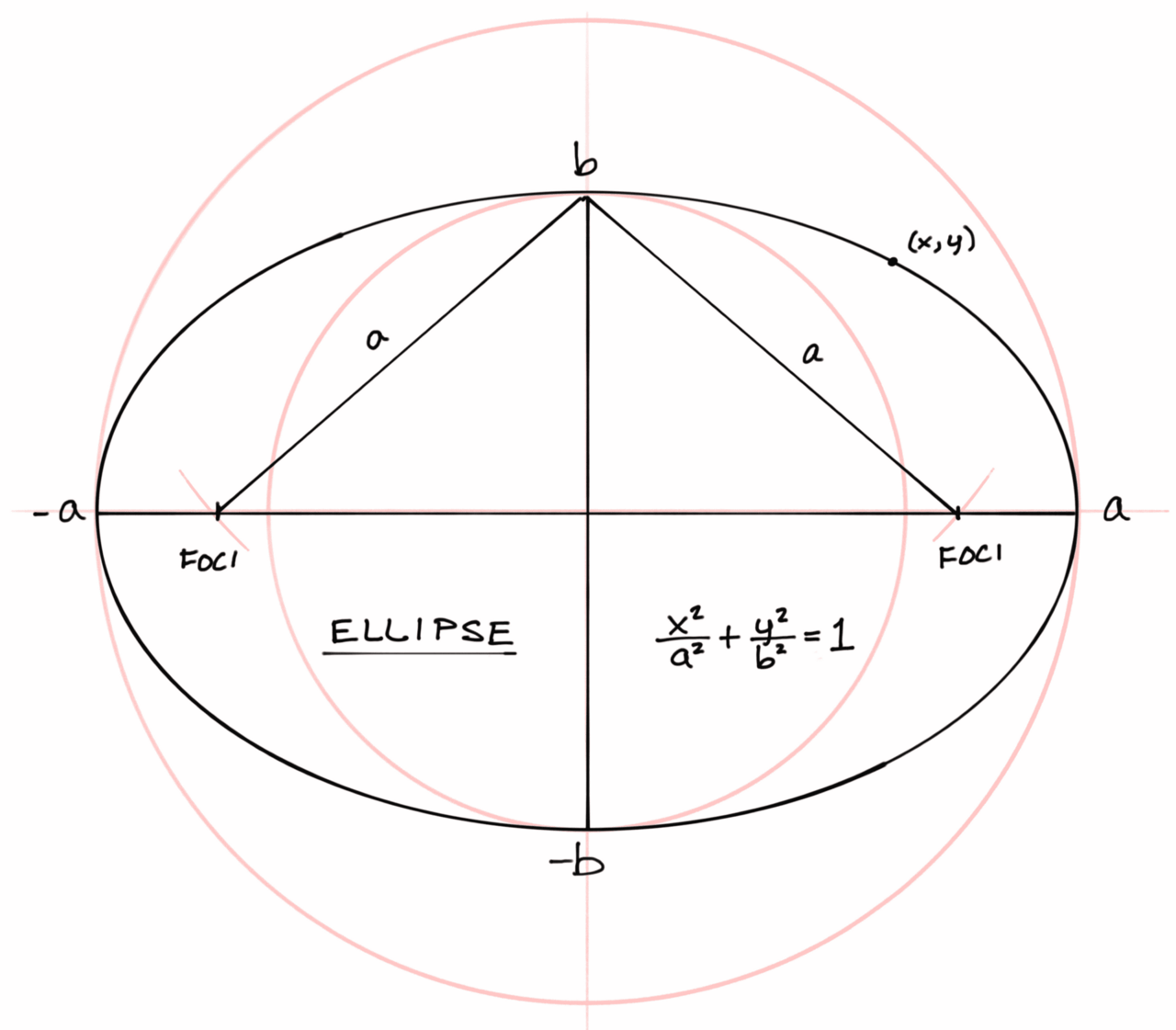
A sketch of the concepts in an ellipse. The focal points (foci) are the major radius (a) distance from the top (b) to an intersection point on the major axis. Distance from foci-to-ellipse-to-foci is always the full length of the major axis. This is why we draw an ellipse using a string and two pins at the foci (see video below).
A clear explanation on why there is no equation for the perimeter of an ellipse plus other facts about ellipse math. He also includes a demonstration of the string method to draw an ellipse. It’s worth watching!